Tutorial 6 - Métodos não supervisionados

Carregando os pacotes

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.cluster import KMeans, DBSCAN
from sklearn.preprocessing import StandardScaler

Lendo os dados

Você pode baixar os dados aqui.

Neste tutorial vamos aprender 2 métodos de machine learning que servem para problemas de agrupamento. Neste tipo de problemas, não temos uma variável de saída conhecida, portanto não podemos usar os métodos supervisionados já conhecidos.

penguins = pd.read_csv('pydata5/penguins.csv')

penguins.head()
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g sex
0 Adelie Torgersen 39.1 18.7 181.0 3750.0 MALE
1 Adelie Torgersen 39.5 17.4 186.0 3800.0 FEMALE
2 Adelie Torgersen 40.3 18.0 195.0 3250.0 FEMALE
3 Adelie Torgersen NaN NaN NaN NaN NaN
4 Adelie Torgersen 36.7 19.3 193.0 3450.0 FEMALE

colunas:

penguins.info()
penguins.isna().sum()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 344 entries, 0 to 343
Data columns (total 7 columns):
 #   Column             Non-Null Count  Dtype  
---  ------             --------------  -----  
 0   species            344 non-null    object 
 1   island             344 non-null    object 
 2   bill_length_mm     342 non-null    float64
 3   bill_depth_mm      342 non-null    float64
 4   flipper_length_mm  342 non-null    float64
 5   body_mass_g        342 non-null    float64
 6   sex                333 non-null    object 
dtypes: float64(4), object(3)
memory usage: 18.9+ KB
species               0
island                0
bill_length_mm        2
bill_depth_mm         2
flipper_length_mm     2
body_mass_g           2
sex                  11
dtype: int64

quantidades:

sns.countplot(x = "species", data = penguins)
plt.show()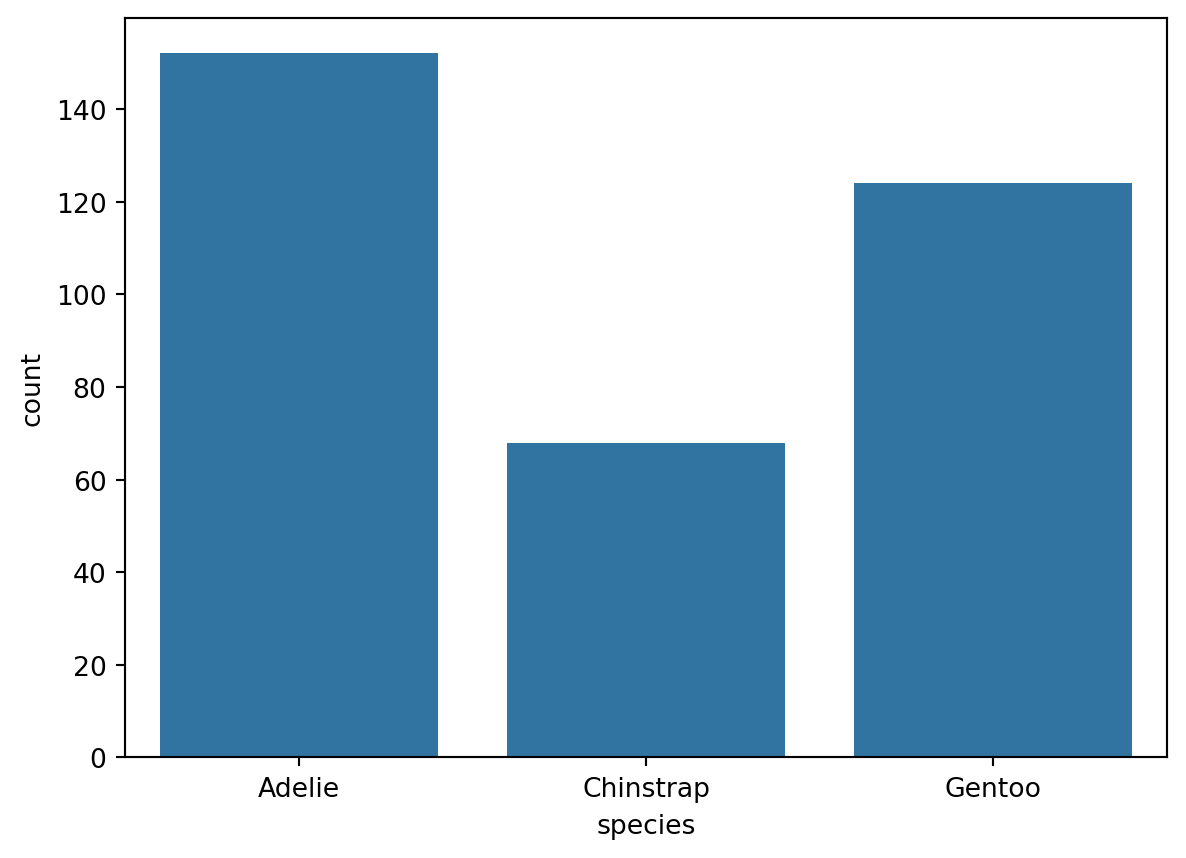

boxplots:

fig,axs = plt.subplots(ncols = 2)
fig.tight_layout()

sns.boxplot(y= 'bill_length_mm', x = 'species', data = penguins, ax= axs[0])
sns.boxplot(y= 'bill_depth_mm', x = 'species', data = penguins, ax= axs[1])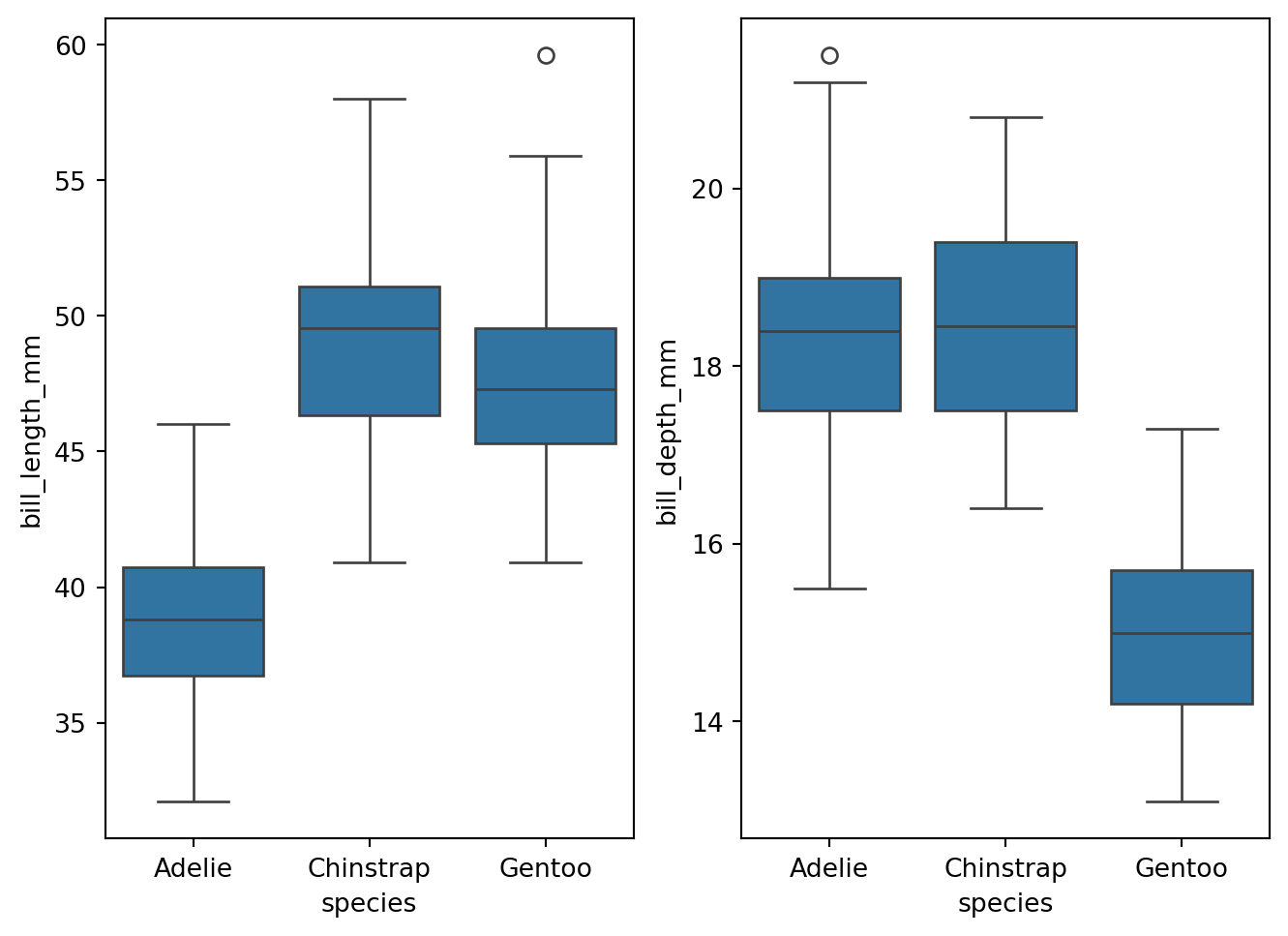

K-means

Vamos aprender inicialmente o método conhecido como ‘k-means’ que basicamente agrupa as observações por uma métrica de similaridade e distância e logo cria os grupos a partir da aproximação entre elas, ou seja, aquelas observações com distância pequena entre elas farão parte do mesmo grupo.

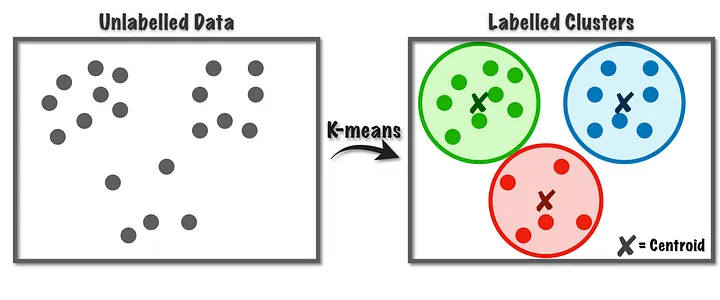
Vamos plotar os dados:

sns.scatterplot(x='bill_length_mm', y='bill_depth_mm', data = penguins)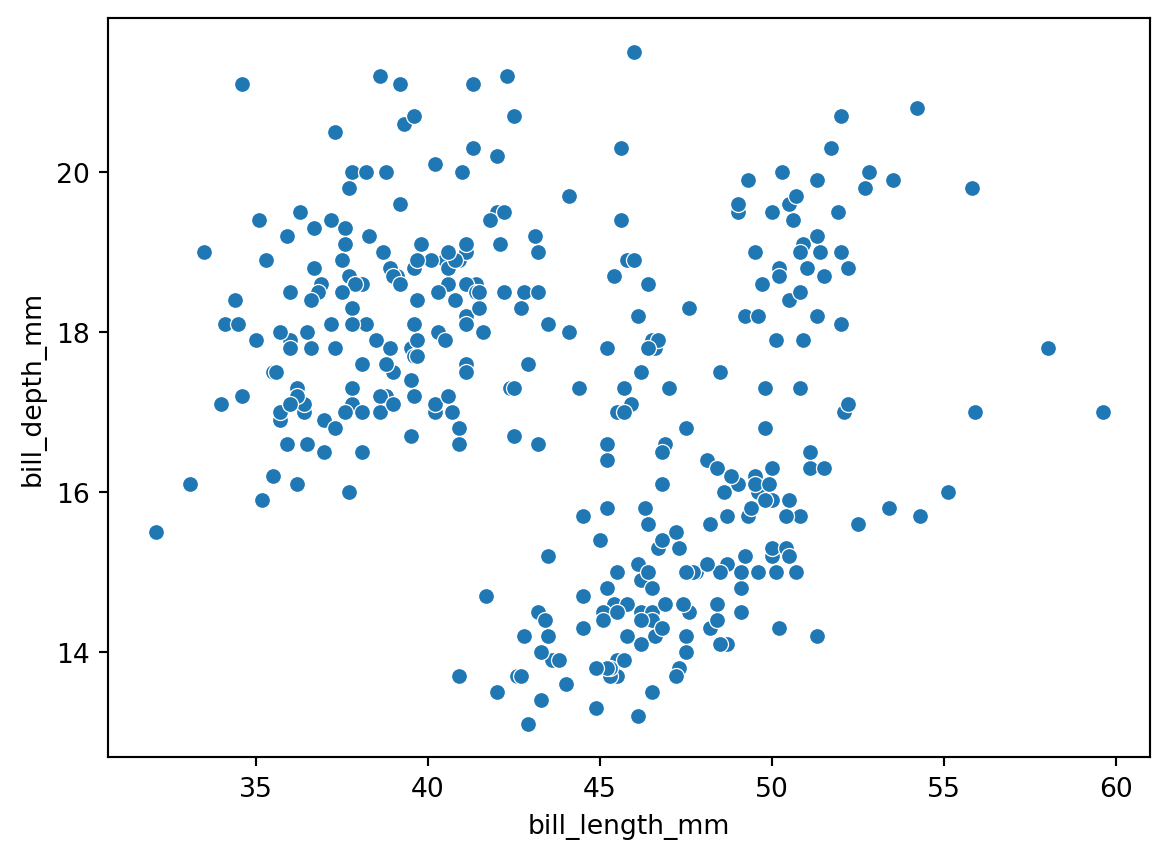

Agora podemos começar o tratamento dos dados.

df = penguins.dropna(inplace=True)
df = penguins.drop(columns=['species', 'island', 'sex'])

df.info()
<class 'pandas.core.frame.DataFrame'>
Index: 333 entries, 0 to 343
Data columns (total 4 columns):
 #   Column             Non-Null Count  Dtype  
---  ------             --------------  -----  
 0   bill_length_mm     333 non-null    float64
 1   bill_depth_mm      333 non-null    float64
 2   flipper_length_mm  333 non-null    float64
 3   body_mass_g        333 non-null    float64
dtypes: float64(4)
memory usage: 13.0 KB

Utilizando o algoritmo de padronização:

scaler = StandardScaler()
scaled_data = scaler.fit_transform(df)

Reconvertendo o dataset scaled_data para dataframe para facilitar o manuseio.

df = pd.DataFrame(scaled_data, columns=df.columns)

df.head()
bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
0 -0.896042 0.780732 -1.426752 -0.568475
1 -0.822788 0.119584 -1.069474 -0.506286
2 -0.676280 0.424729 -0.426373 -1.190361
3 -1.335566 1.085877 -0.569284 -0.941606
4 -0.859415 1.747026 -0.783651 -0.692852 
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 333 entries, 0 to 332
Data columns (total 4 columns):
 #   Column             Non-Null Count  Dtype  
---  ------             --------------  -----  
 0   bill_length_mm     333 non-null    float64
 1   bill_depth_mm      333 non-null    float64
 2   flipper_length_mm  333 non-null    float64
 3   body_mass_g        333 non-null    float64
dtypes: float64(4)
memory usage: 10.5 KB

Rodando o algoritmo k-means:

kmeans = KMeans(n_clusters=3, random_state=42, n_init=10)
kmeans.fit(df)
KMeans(n_clusters=3, n_init=10, random_state=42)
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

incluindo a coluna cluster:

df['cluster'] = kmeans.labels_

df.head()

df.tail()
bill_length_mm bill_depth_mm flipper_length_mm body_mass_g cluster
328 0.587352 -1.762145 0.931283 0.892957 1
329 0.514098 -1.457000 1.002739 0.799674 1
330 1.173384 -0.744994 1.502928 1.919069 1
331 0.221082 -1.202712 0.788372 1.234995 1
332 1.081817 -0.541564 0.859828 1.483749 1 
sns.scatterplot(x='bill_length_mm', y='bill_depth_mm', hue = 'cluster', data = df)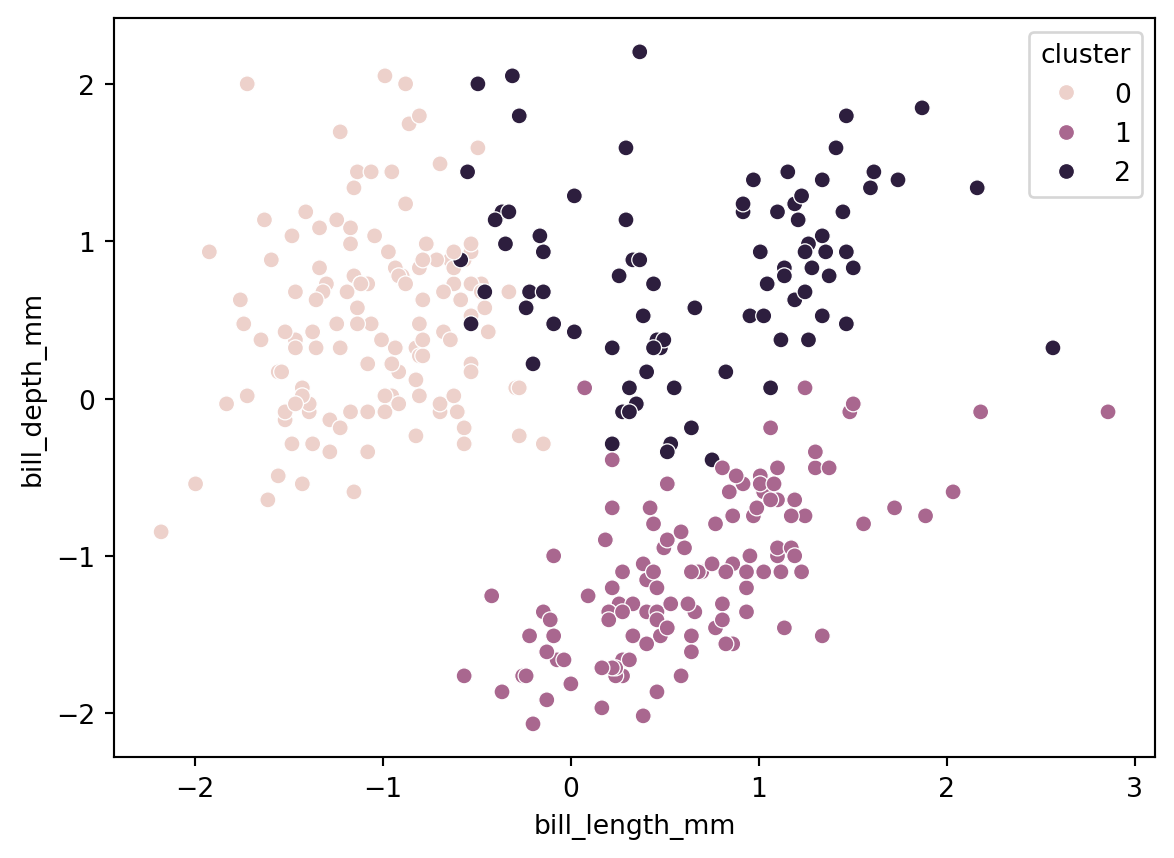

Escolhendo o número ideal de clusters

inertia = []
for i in range(1, 11):
    kmeans = KMeans(n_clusters=i, random_state=i, n_init=10)
    kmeans.fit(df)
    inertia.append(kmeans.inertia_)

Criar um dataframe com todos os valores de k :

inertia_df = pd.DataFrame({'k': range(1, 11), 'inertia': inertia})

inertia_df.head()
k inertia
0 1 1540.186186
1 2 757.624293
2 3 370.766144
3 4 293.904751
4 5 249.413429

Escolhe-se o ponto onde o ‘cotovelo’ é mais visível, neste caso, 3 clusters:

plt.plot(inertia_df['k'], inertia_df['inertia'])
plt.show()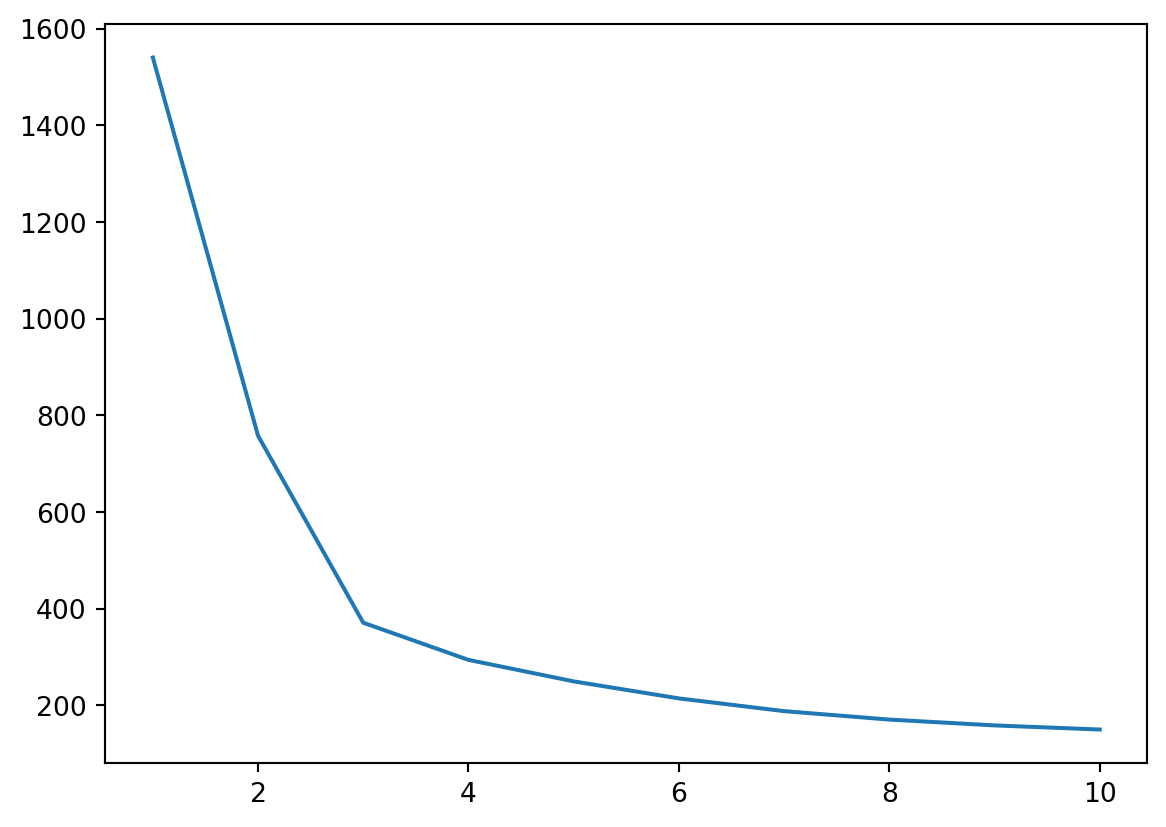

Cluster Hierárquico

A diferença com o método anterior é que para o cluster hierárquico não é necessário pré-definir o número de clusters, pois o método agrupa as observações de forma sequencial, facilitando a identificação do número ideal de cluster.

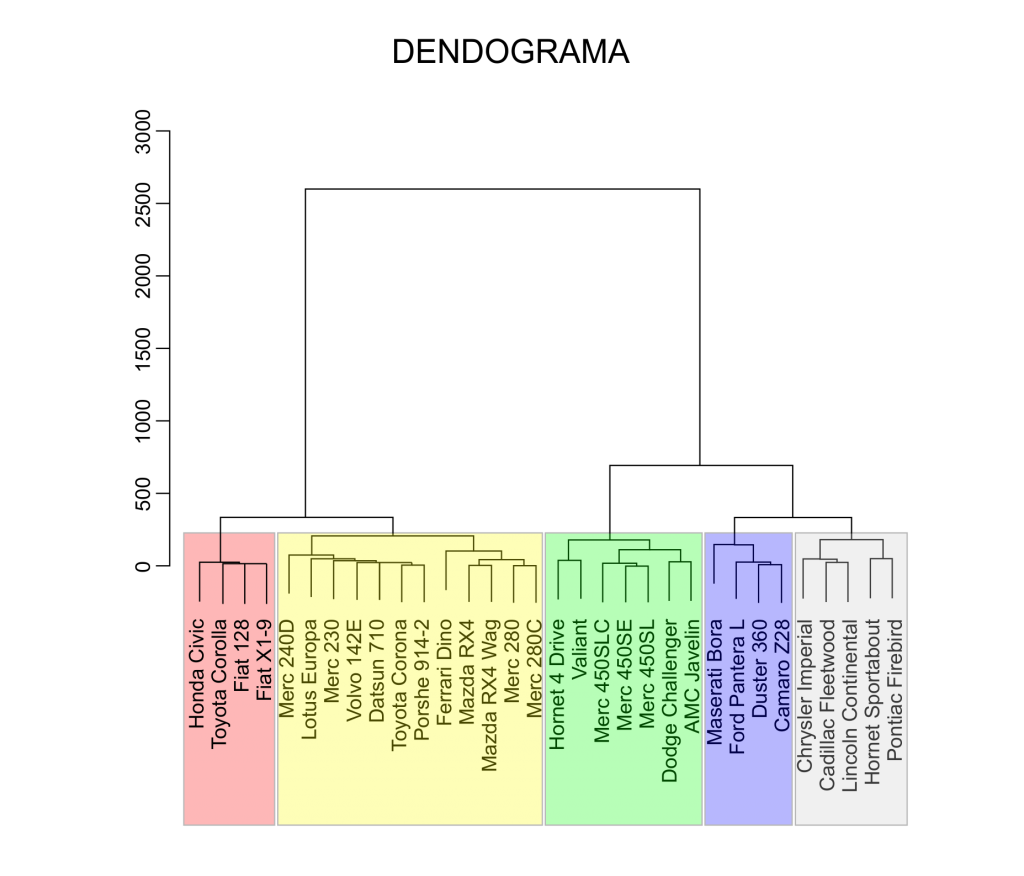
O ideal é que os dados estejam normalizados, pelo menos as colunas numéricas, pois este método aceita também colunas (atributos) categóricos.

from scipy.cluster.hierarchy import linkage, dendrogram

aplicando o algoritmo:

h_clustering = linkage(scaled_data, method="ward", metric="euclidean")

graficando o dendograma:

dendrogram(h_clustering)
plt.show()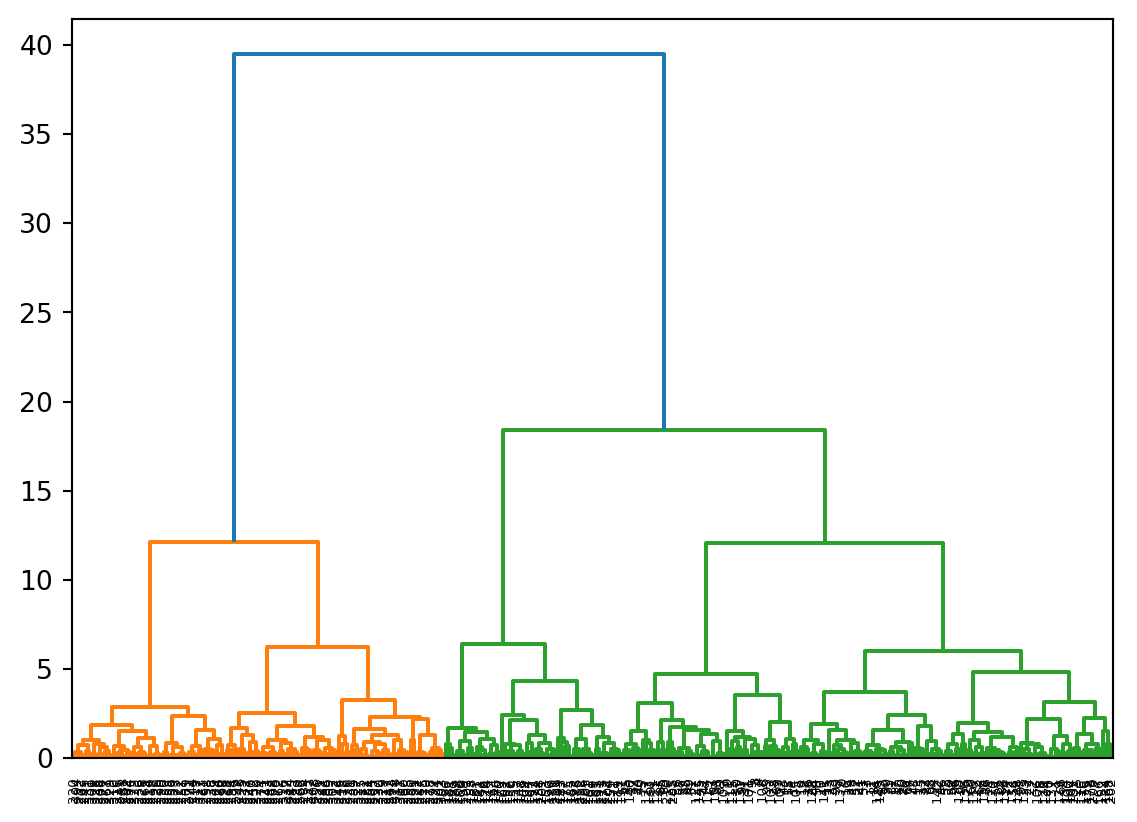

salvando os resultados no dataframe:

from sklearn.cluster import AgglomerativeClustering

cluster = AgglomerativeClustering(n_clusters=3, metric='euclidean', linkage='ward')
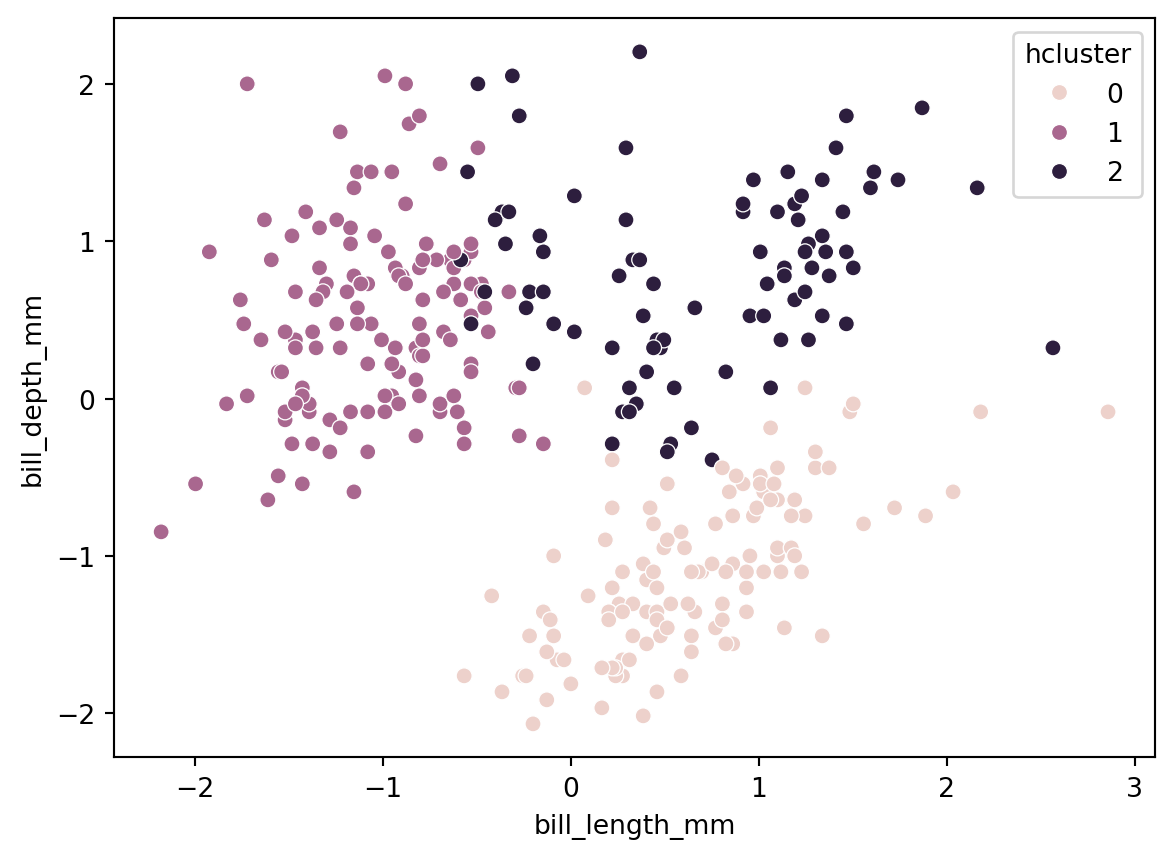
df['hcluster'] = cluster.fit_predict(df)

graficando os resultados:

sns.scatterplot(x='bill_length_mm', y='bill_depth_mm', hue = 'hcluster', data = df)