Tutorial 8 - Métodos de Classificação

Carregando os pacotes

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.model_selection import train_test_split
from sklearn import preprocessing

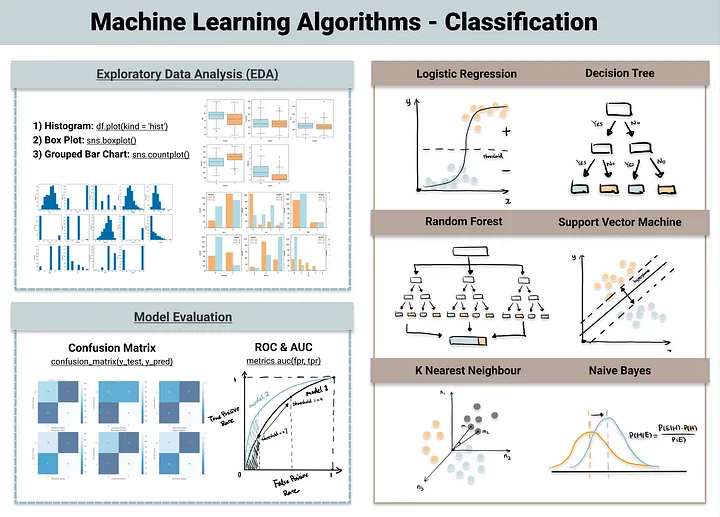
Classificação

Em machine learning, um problema de classificação é a tarefa de ensinar um computador a categorizar um item em uma de várias classes ou grupos pré-definidos, com base em suas características. Imagine que você tem um conjunto de dados históricos, como e-mails já rotulados como “spam” ou “não spam”, ou peças de um motor identificadas como “aptas” ou “defeituosas”. O algoritmo aprende os padrões nesses dados para construir um modelo. O objetivo final é que esse modelo, ao receber um novo e-mail ou os dados de uma nova peça, consiga prever com alta precisão a qual classe ele pertence. Essencialmente, a classificação responde à pergunta: “A qual categoria este item pertence?”.

O problema de classificação em ML. Fonte: Gong (2022)

Os algoritmos

1. Regressão Logística

Regressão Logística. Fonte: Gong (2022)

A Regressão Logística usa a função sigmoide para retornar a probabilidade de um rótulo. Ela é muito utilizada quando o problema de classificação é binário — por exemplo, verdadeiro ou falso, ganhar ou perder, positivo ou negativo.

A função sigmoide gera um valor de probabilidade e, ao compará-lo com um limiar (threshold) pré-definido, o item é classificado com o rótulo correspondente.

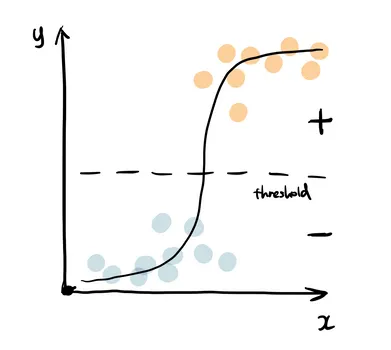
2. Árvore de Decisão

Árvore de Decisão. Fonte: Gong (2022)

A Árvore de Decisão cria seus ramos de forma hierárquica, onde cada ramo pode ser entendido como uma estrutura condicional if-else.

Os ramos são desenvolvidos dividindo-se o conjunto de dados (dataset) em subconjuntos, com base nas características (features) de maior importância. A classificação final ocorre nas folhas da árvore.

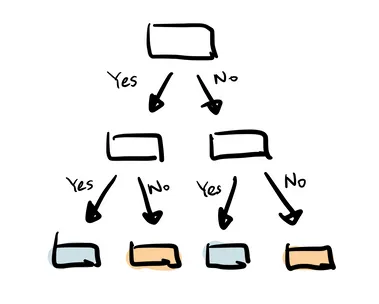
3. Random Forest

Random Forests. Fonte: Gong (2022)

Como o próprio nome sugere, o Random Forest (ou Floresta Aleatória) é um conjunto de árvores de decisão. É um tipo comum de método de ensemble, que agrega os resultados de múltiplos preditores.

O Random Forest utiliza adicionalmente a técnica de bagging, que permite que cada árvore seja treinada com uma amostragem aleatória do conjunto de dados original e, ao final, considera o voto da maioria das árvores para o resultado.

Em comparação com uma única árvore de decisão, este método tem uma melhor generalização, mas é menos interpretável, devido às múltiplas camadas de complexidade adicionadas ao modelo.

Lendo os dados

df = pd.read_csv('pydata5/card_transdata.csv')

df = df.sample(10000).copy()

df.head(10)

	distance_from_home	distance_from_last_transaction	ratio_to_median_purchase_price	repeat_retailer	used_chip	used_pin_number	online_order	fraud
486856	9.214883	0.431098	0.314582	1.0	1.0	0.0	1.0	0.0
515789	11.667397	0.089375	1.406865	1.0	0.0	1.0	1.0	0.0
443778	22.532558	1.506233	0.404679	1.0	1.0	0.0	1.0	0.0
398263	12.377269	0.179923	1.373075	1.0	0.0	0.0	1.0	0.0
887112	4.046479	0.049327	0.505305	1.0	0.0	0.0	1.0	0.0
92342	196.562848	66.249490	0.189499	1.0	0.0	0.0	1.0	1.0
755895	9.842020	77.916720	1.805561	1.0	0.0	1.0	0.0	0.0
654083	39.544694	3.382505	4.591887	1.0	0.0	0.0	1.0	1.0
199387	26.615302	4.439700	1.520829	1.0	1.0	0.0	1.0	0.0
516171	13.182010	8.921574	1.021895	1.0	1.0	0.0	1.0	0.0

df.info()

<class 'pandas.core.frame.DataFrame'>
Index: 10000 entries, 486856 to 21156
Data columns (total 8 columns):
 #   Column                          Non-Null Count  Dtype  
---  ------                          --------------  -----  
 0   distance_from_home              10000 non-null  float64
 1   distance_from_last_transaction  10000 non-null  float64
 2   ratio_to_median_purchase_price  10000 non-null  float64
 3   repeat_retailer                 10000 non-null  float64
 4   used_chip                       10000 non-null  float64
 5   used_pin_number                 10000 non-null  float64
 6   online_order                    10000 non-null  float64
 7   fraud                           10000 non-null  float64
dtypes: float64(8)
memory usage: 703.1 KB

df.describe()

	distance_from_home	distance_from_last_transaction	ratio_to_median_purchase_price	repeat_retailer	used_chip	used_pin_number	online_order	fraud
count	10000.000000	10000.000000	10000.000000	10000.000000	10000.000000	10000.000000	10000.000000	10000.000000
mean	26.629818	5.456363	1.872987	0.879200	0.351200	0.099400	0.650300	0.090200
std	67.546517	24.969811	2.957269	0.325911	0.477369	0.299213	0.476899	0.286482
min	0.037396	0.001225	0.013200	0.000000	0.000000	0.000000	0.000000	0.000000
25%	3.848924	0.283383	0.475306	1.000000	0.000000	0.000000	0.000000	0.000000
50%	9.873617	0.994411	1.013134	1.000000	0.000000	0.000000	1.000000	0.000000
75%	25.464573	3.432359	2.134546	1.000000	1.000000	0.000000	1.000000	0.000000
max	3243.926263	1261.525290	62.227930	1.000000	1.000000	1.000000	1.000000	1.000000

df.query('distance_from_home > 1000')

	distance_from_home	distance_from_last_transaction	ratio_to_median_purchase_price	repeat_retailer	used_chip	used_pin_number	online_order	fraud
915645	1741.752772	0.660238	0.792538	1.0	0.0	1.0	0.0	0.0
297794	1464.765479	11.120252	0.289282	1.0	0.0	0.0	1.0	1.0
475654	3243.926263	0.962096	2.584001	1.0	1.0	0.0	1.0	0.0
507911	1204.761613	351.530503	0.502558	1.0	0.0	0.0	0.0	1.0
89453	1005.276050	3.224338	0.903404	1.0	0.0	0.0	1.0	1.0
740780	1031.638377	45.573304	0.376136	1.0	0.0	0.0	0.0	0.0

Análise exploratória

colors = ['#d62828', '#f77f00', '#003049']

num_list = ['distance_from_home', 'distance_from_last_transaction', 'ratio_to_median_purchase_price']
fig, axes = plt.subplots(nrows=3, ncols=1, figsize=(8, 10))

for i, column in enumerate(num_list):
  df[column].plot(kind='kde', ax=axes[i], color=colors[i], lw=3)
  axes[i].set_title(f'Distribuição de "{column}"', fontsize=14)
  axes[i].set_xlabel('')
  axes[i].set_xscale('log')
  
plt.tight_layout()
plt.show()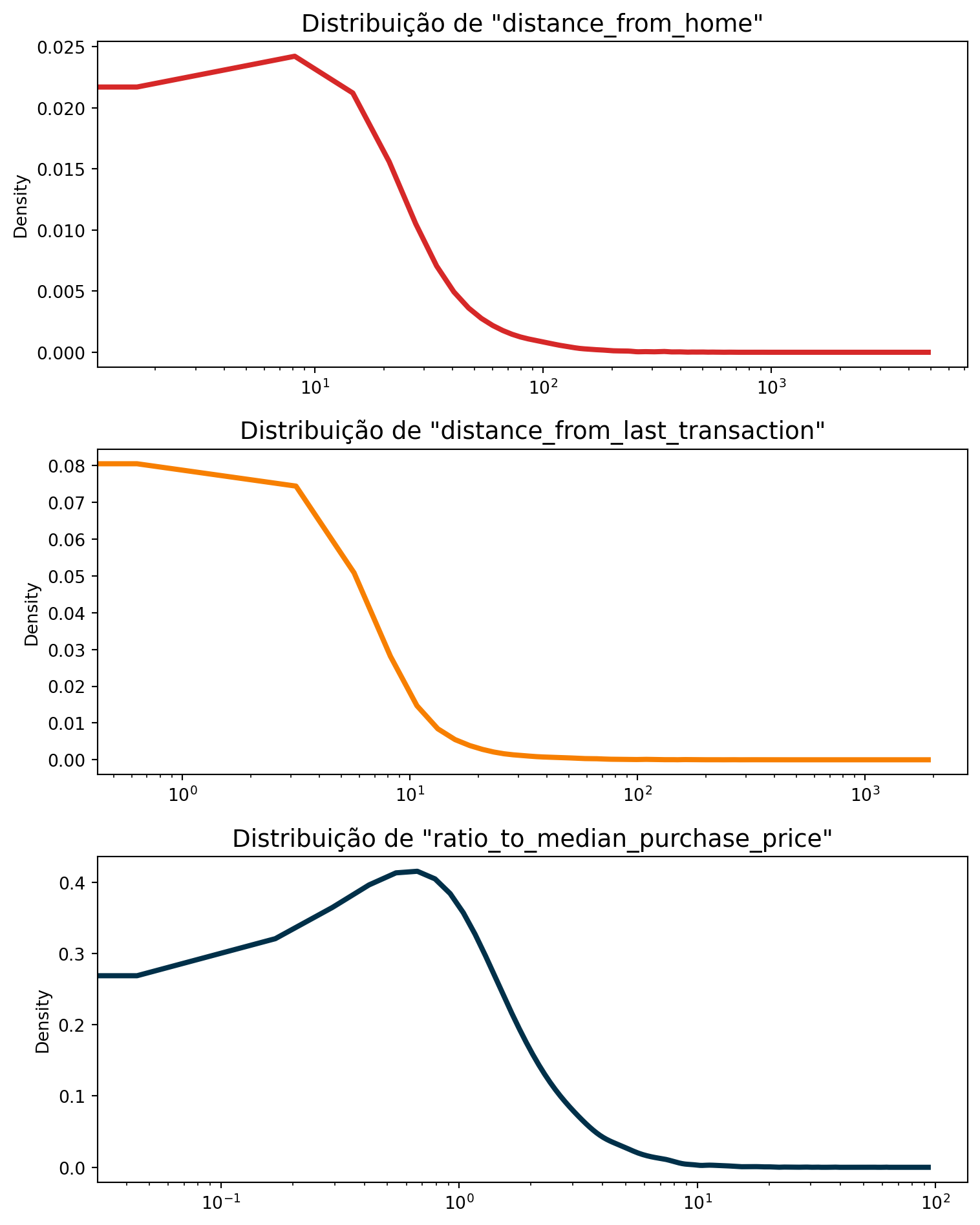

Features Categóricas e o target:

cat_list = ['repeat_retailer','used_chip','used_pin_number','online_order']
fig = plt.figure(figsize=(8,4))

for i in range(len(cat_list)):
  column = cat_list[i]
  sub = fig.add_subplot(2,2, i+1)
  chart = sns.countplot(data=df, x=column, hue='fraud', palette = colors[0:2])

plt.tight_layout()
plt.show()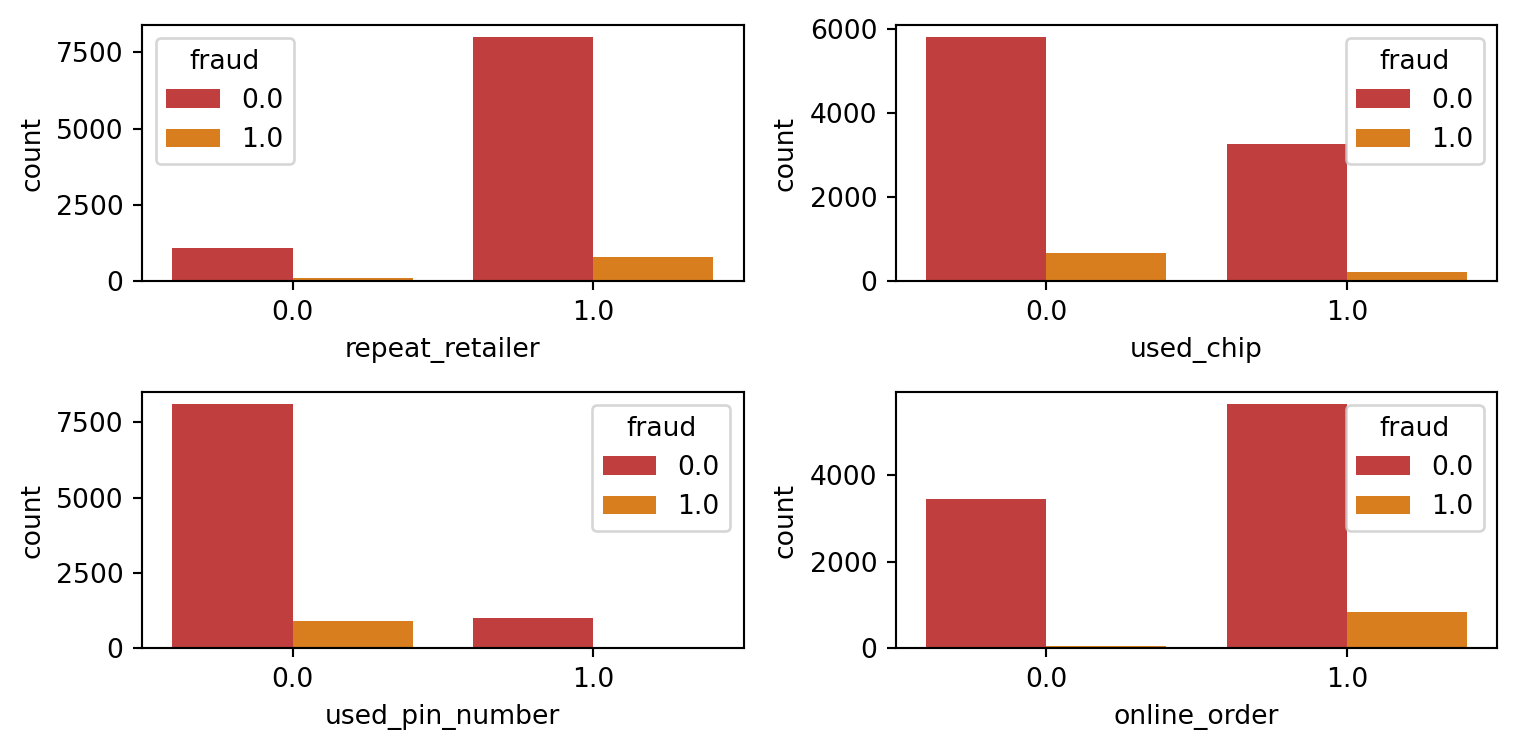

Features numéricas e o target:

fig = plt.figure(figsize = (6,12))
for i, column in enumerate(num_list):
  
  ax = fig.add_subplot(3, 1, i + 1)
  sns.boxplot(x='fraud', y=column, data=df, hue='fraud', palette=colors[0:2], ax=ax)
  ax.set_yscale('log')
  ax.set_title(f'Distribuição de "{column}" por Fraude (Escala Log)', fontsize=14)

plt.tight_layout()

plt.show()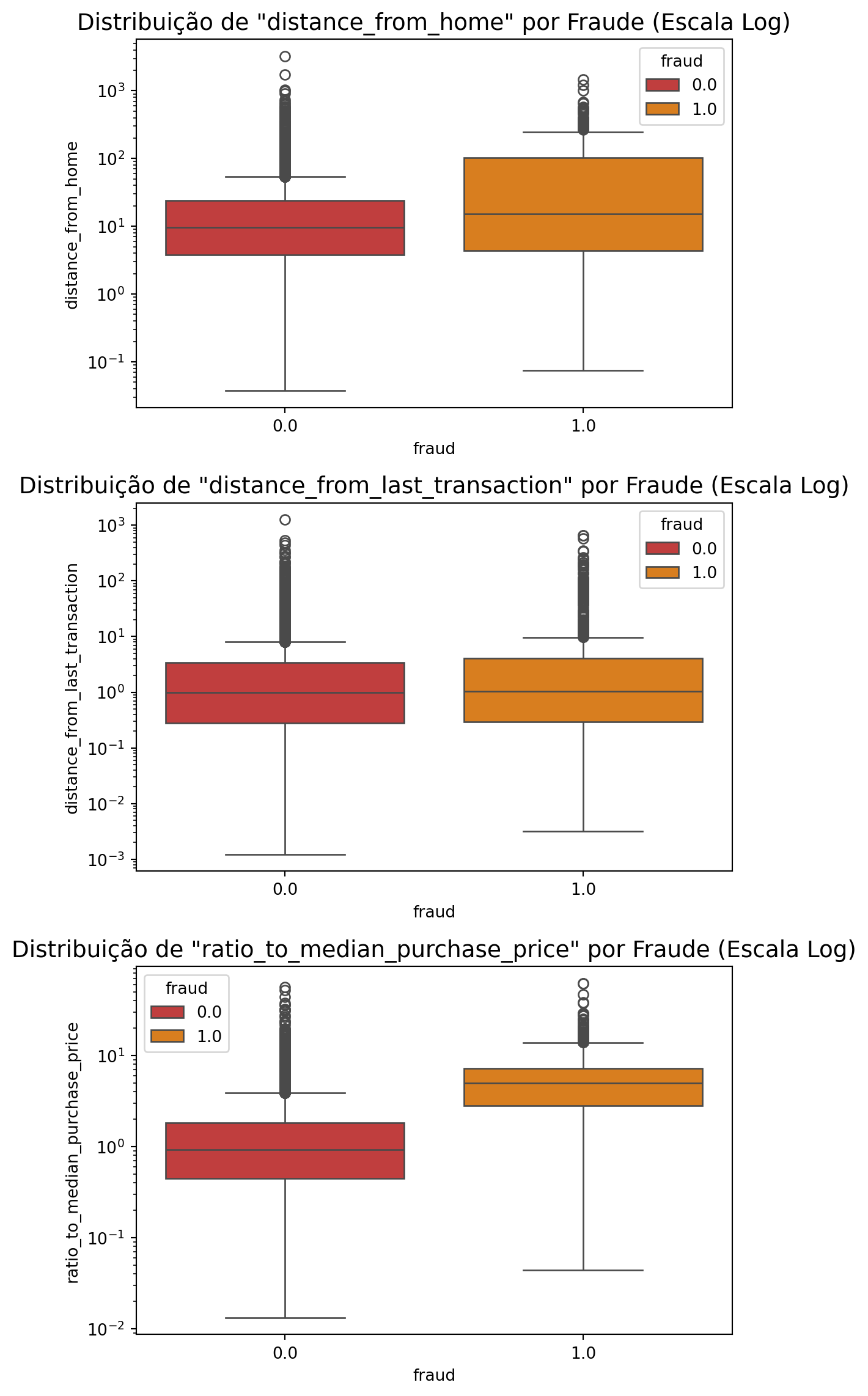

Split dataset

X = df.drop(['fraud'], axis=1)
y = df["fraud"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=2025)

Regressão Logística

from sklearn.linear_model import LogisticRegression

Para modelos com poucas observações usar solver='liblinear', já para modelos com datasets grandes, usar solver='saga'.

modelo_logreg = LogisticRegression(
    solver='liblinear', 
    n_jobs=-1,
    random_state=42,
    max_iter=5000 
)

# Medir o tempo de treinamento

#start_time = time.time()
modelo_logreg.fit(X_train, y_train)
#end_time = time.time()
#training_time = end_time - start_time

/Users/mauricio/Library/Python/3.8/lib/python/site-packages/sklearn/linear_model/_logistic.py:1223: UserWarning:

'n_jobs' > 1 does not have any effect when 'solver' is set to 'liblinear'. Got 'n_jobs' = 10.

LogisticRegression(max_iter=5000, n_jobs=-1, random_state=42,
                   solver='liblinear')

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Fazer Previsões com os Dados de Teste:

y_pred_logreg = modelo_logreg.predict(X_test)

Avaliação do Modelo

A Acurácia é o indicador mais direto do desempenho do modelo. Ela mede o percentual de previsões corretas:

$$A=\frac{TP+TN}{TP+FP+FN+TN}$$

Agora vamos calcular alguns indicadores de acurácia.

from sklearn.metrics import accuracy_score, confusion_matrix, classification_report, roc_curve, roc_auc_score

acuracia_logreg = accuracy_score(y_test, y_pred_logreg)
print(f"\nAcurácia do modelo: {acuracia_logreg:.4f}")

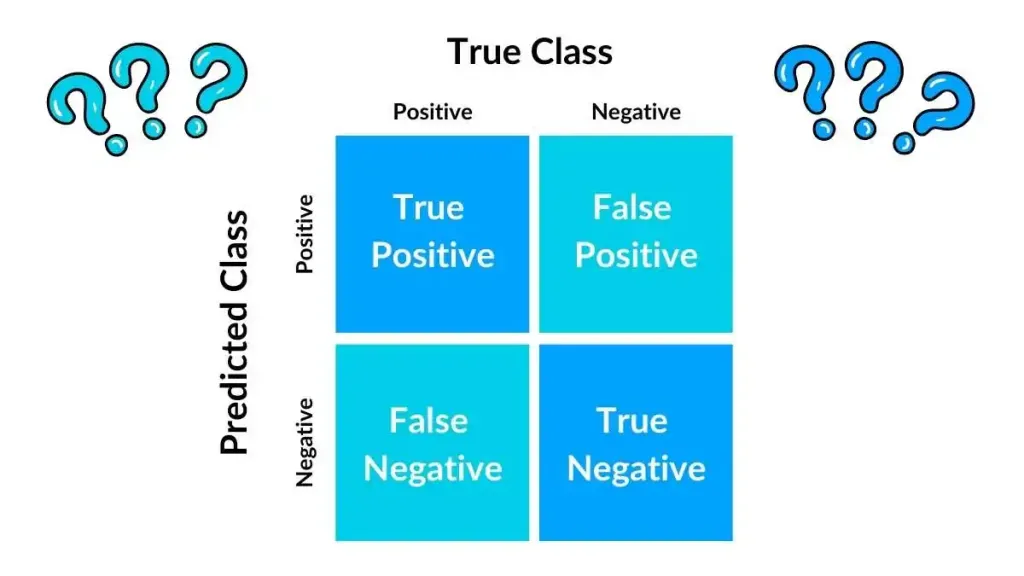
Acurácia do modelo: 0.9430

Outro indicador da acurácia diz respeito às vezes que o modelo acertou, para isto é necessário calcular a Matriz de Confusão.

Matriz de Confusão. Fonte: van Otten (2024)

cm_log_reg = confusion_matrix(y_test, y_pred_logreg)

plt.figure(figsize=(8, 6))
sns.heatmap(
    cm_log_reg, 
    annot=True,
    fmt='d', 
    cmap='Reds',
    xticklabels=['Classe 0', 'Classe 1'],
    yticklabels=['Classe 0', 'Classe 1']
)
plt.title('Matriz de Confusão', fontsize=16)
plt.ylabel('Rótulo Verdadeiro', fontsize=12)
plt.xlabel('Rótulo Previsto', fontsize=12)
plt.show()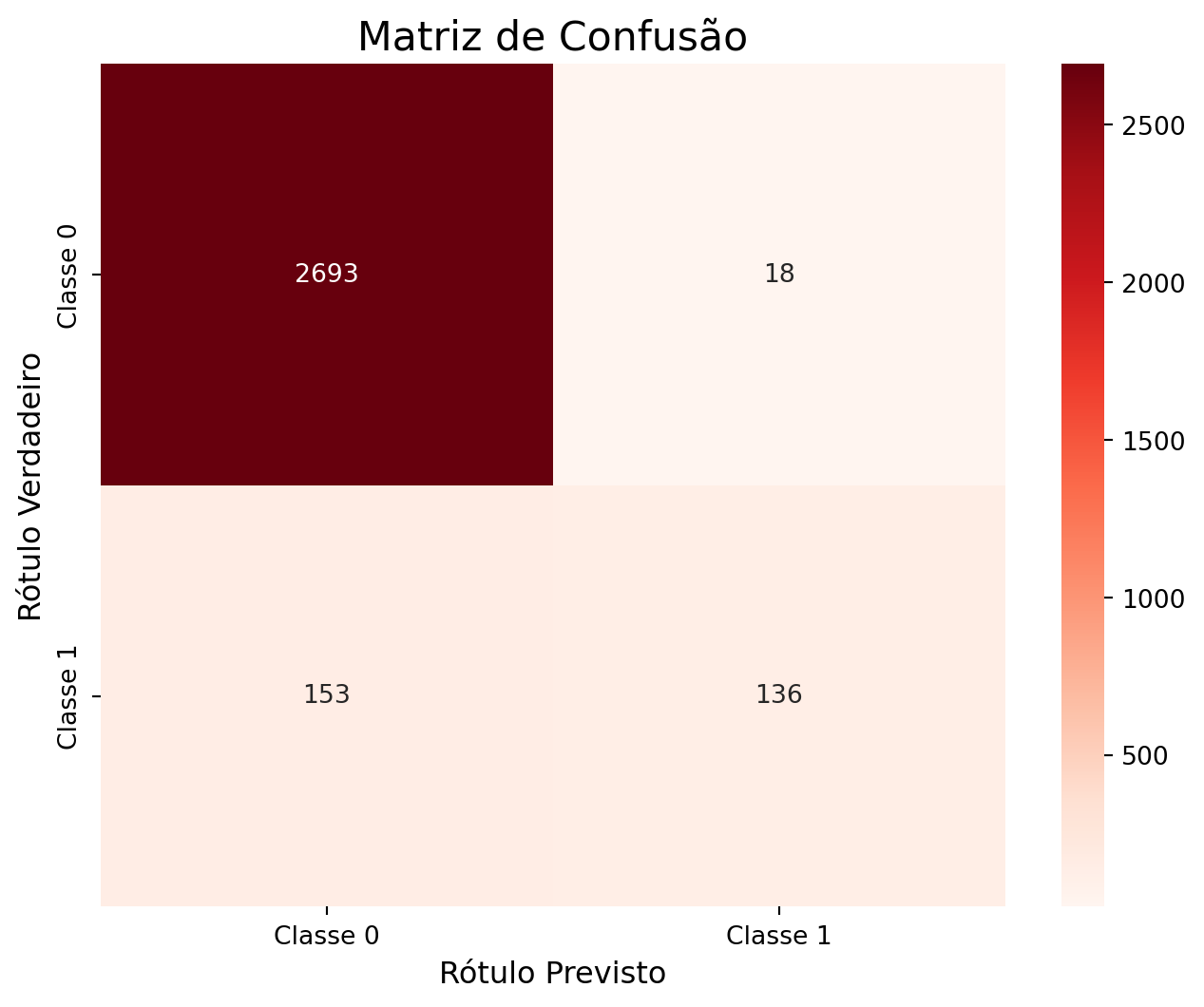

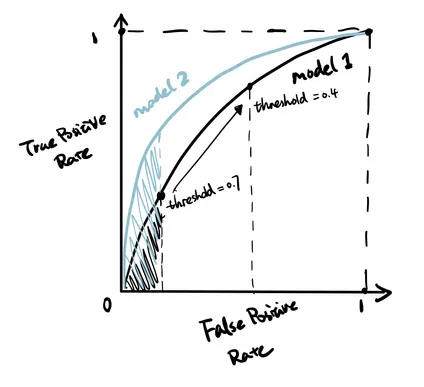
O próximo indicador é o AUC (área sob a curva) que é calculada a partir da ROC (curva característica do processo). Imagine que você está avaliando um médico.

Curva ROC. Fonte: Gong (2022)

A Curva ROC é um gráfico que mostra o quão bom o médico (seu modelo) é em fazer diagnósticos. Ela mostra o equilíbrio entre duas coisas:

1. Acertar os doentes (Eixo Y): A taxa de “Verdadeiros Positivos”. O ideal é que seja alta.

2. Errar com os saudáveis (Eixo X): A taxa de “Falsos Positivos”, ou seja, quantas vezes ele diagnostica a doença em quem não a tem. O ideal é que seja baixa.

O objetivo é ter uma curva que “suba rápido” e fique o mais próximo possível do canto superior esquerdo, o que significa acertar muitos doentes sem errar muito com os saudáveis.

A AUC (Área Sob a Curva) é a nota final que o médico recebe, resumindo o gráfico inteiro em um único número.

• $AUC=1.0$: Um médico perfeito. Nunca erra.
• $AUC>0.8$: Um médico excelente, muito confiável.
• $AUC=0.5$: Um médico inútil. O desempenho dele é igual a jogar uma moeda para decidir.

Em resumo: A Curva ROC é o relatório de desempenho completo, e a AUC é a nota final que diz, de 0.5 a 1.0, o quão bom seu modelo é em separar as classes.

Para obter o valor de AUC, é necessário calcular as probabilidades:

y_pred_logreg_proba = modelo_logreg.predict_proba(X_test)[:, 1]

auc_score_logreg = roc_auc_score(y_test, y_pred_logreg_proba)
print(f"Pontuação ROC AUC: {auc_score_logreg:.4f}")

Pontuação ROC AUC: 0.9635

Calcular a curva ROC:

fpr, tpr, thresholds = roc_curve(y_test, y_pred_logreg_proba)

plt.figure(figsize=(8, 4))
# Plotar a curva do nosso modelo
plt.plot(fpr, tpr, color=colors[0], lw=2, label=f'Curva ROC (AUC = {auc_score_logreg:.4f})')
# Plotar a linha de referência de um classificador aleatório (AUC = 0.5)
plt.plot([0, 1], [0, 1], color=colors[1], lw=2, linestyle='--', label='Classificador Aleatório')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('Taxa de Falsos Positivos (FPR)', fontsize=12)
plt.ylabel('Taxa de Verdadeiros Positivos (TPR)', fontsize=12)
plt.title('Curva ROC (Receiver Operating Characteristic)', fontsize=16)
plt.legend(loc="lower right")
plt.tight_layout()
plt.show()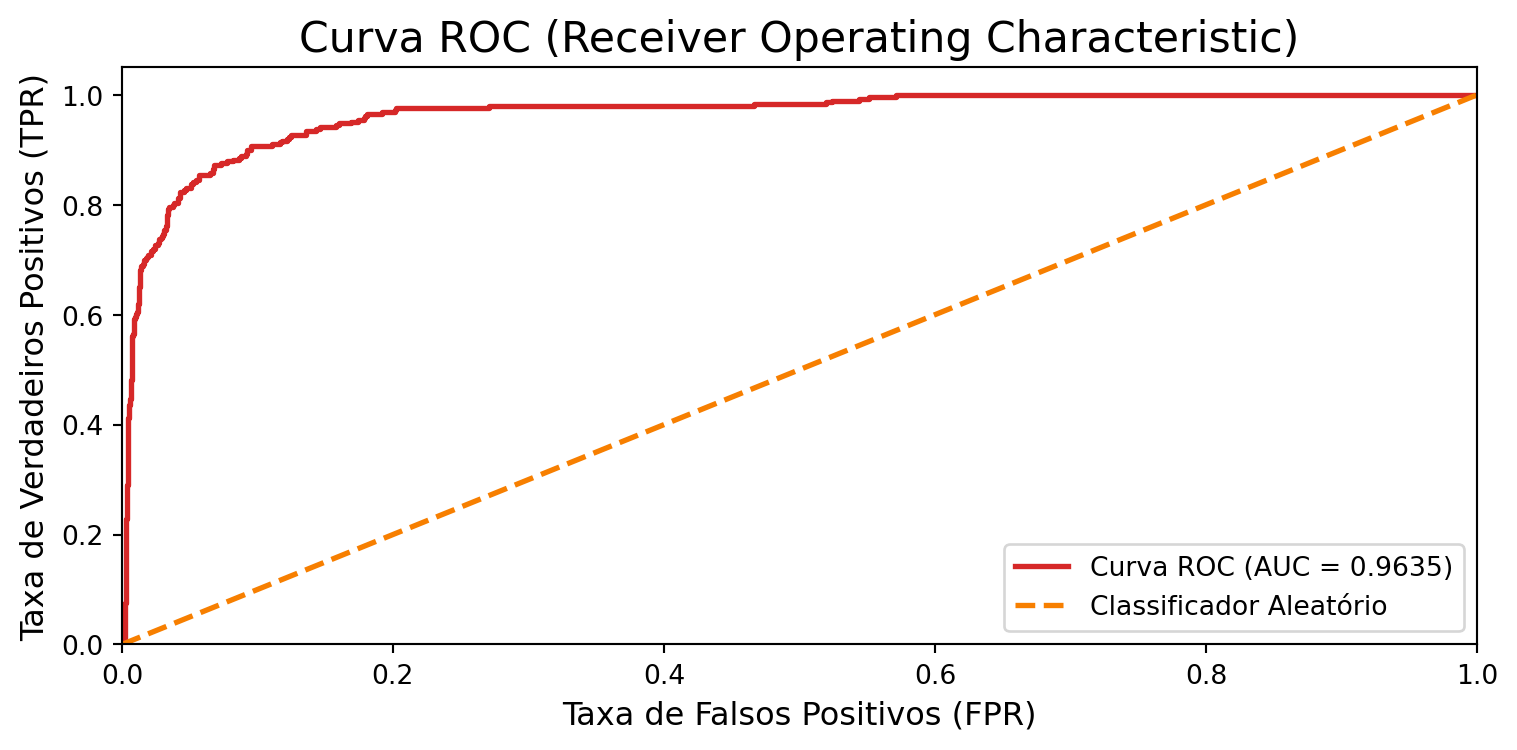

Árvore de Decisão

from sklearn.tree import DecisionTreeClassifier, plot_tree

Vamos treinar o modelo:

modelo_tree = DecisionTreeClassifier(
    max_depth=6,
    class_weight='balanced',
    random_state=2025
)

modelo_tree.fit(X_train, y_train)

DecisionTreeClassifier(class_weight='balanced', max_depth=6, random_state=2025)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Fazemos as previsões:

y_pred_tree = modelo_tree.predict(X_test)
y_pred_tree_proba = modelo_tree.predict_proba(X_test)[:, 1] #classe com fraude

Avaliação do Modelo

acuracia_tree = accuracy_score(y_test, y_pred_tree)
print(f"\nAcurácia do modelo: {acuracia_tree:.4f}")

Acurácia do modelo: 0.9953

auc_score_tree = roc_auc_score(y_test, y_pred_tree_proba)
print(f"Pontuação ROC AUC: {auc_score_tree:.4f}")

Pontuação ROC AUC: 0.9911

E a curva ROC:

fpr, tpr, thresholds = roc_curve(y_test, y_pred_tree_proba)

plt.figure(figsize=(8, 8))
plt.plot(fpr, tpr, color=colors[0], lw=2, label=f'Curva ROC (AUC = {auc_score_tree:.4f})')
plt.plot([0, 1], [0, 1], color=colors[1], lw=2, linestyle='--', label='Classificador Aleatório')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('Taxa de Falsos Positivos (FPR)', fontsize=12)
plt.ylabel('Taxa de Verdadeiros Positivos (TPR)', fontsize=12)
plt.title('Curva ROC (Receiver Operating Characteristic)', fontsize=16)
plt.legend(loc="lower right")
plt.tight_layout()
plt.show()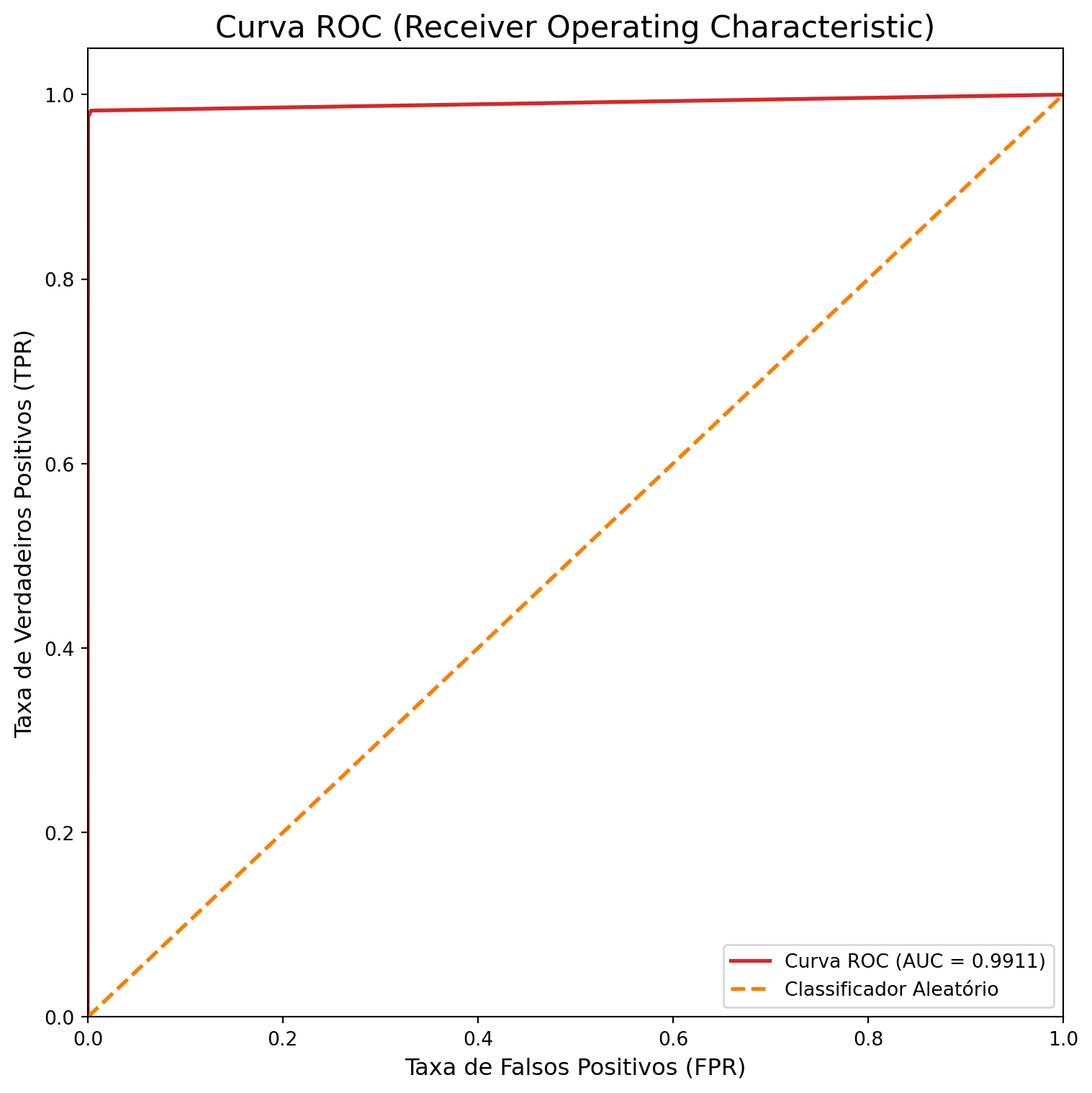

Random Forest

from sklearn.ensemble import RandomForestClassifier

construimos o modelo:

modelo_rf = RandomForestClassifier(
    n_estimators=100,
    class_weight='balanced',
    random_state=42,
    n_jobs=-1)

treinamos o modelo:

modelo_rf.fit(X_train, y_train)

RandomForestClassifier(class_weight='balanced', n_jobs=-1, random_state=42)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

construimos as previsões:

y_pred_rf = modelo_rf.predict(X_test)
y_pred_rf_proba = modelo_rf.predict_proba(X_test)[:, 1]

Avaliação do Modelo

acuracia_rf = accuracy_score(y_test, y_pred_rf)
print(f"\nAcurácia do modelo: {acuracia_rf:.4f}")

Acurácia do modelo: 0.9970

auc_score_rf = roc_auc_score(y_test, y_pred_rf_proba)
print(f"Pontuação ROC AUC: {auc_score_rf:.8f}")

Pontuação ROC AUC: 0.99959412

Matriz de confusão:

cm_rf = confusion_matrix(y_test, y_pred_rf)

plt.figure(figsize=(8, 6))
sns.heatmap(
    cm_rf, 
    annot=True,
    fmt='d', 
    cmap='Reds',
    xticklabels=['Classe 0', 'Classe 1'],
    yticklabels=['Classe 0', 'Classe 1']
)
plt.title('Matriz de Confusão', fontsize=16)
plt.ylabel('Rótulo Verdadeiro', fontsize=12)
plt.xlabel('Rótulo Previsto', fontsize=12)
plt.show()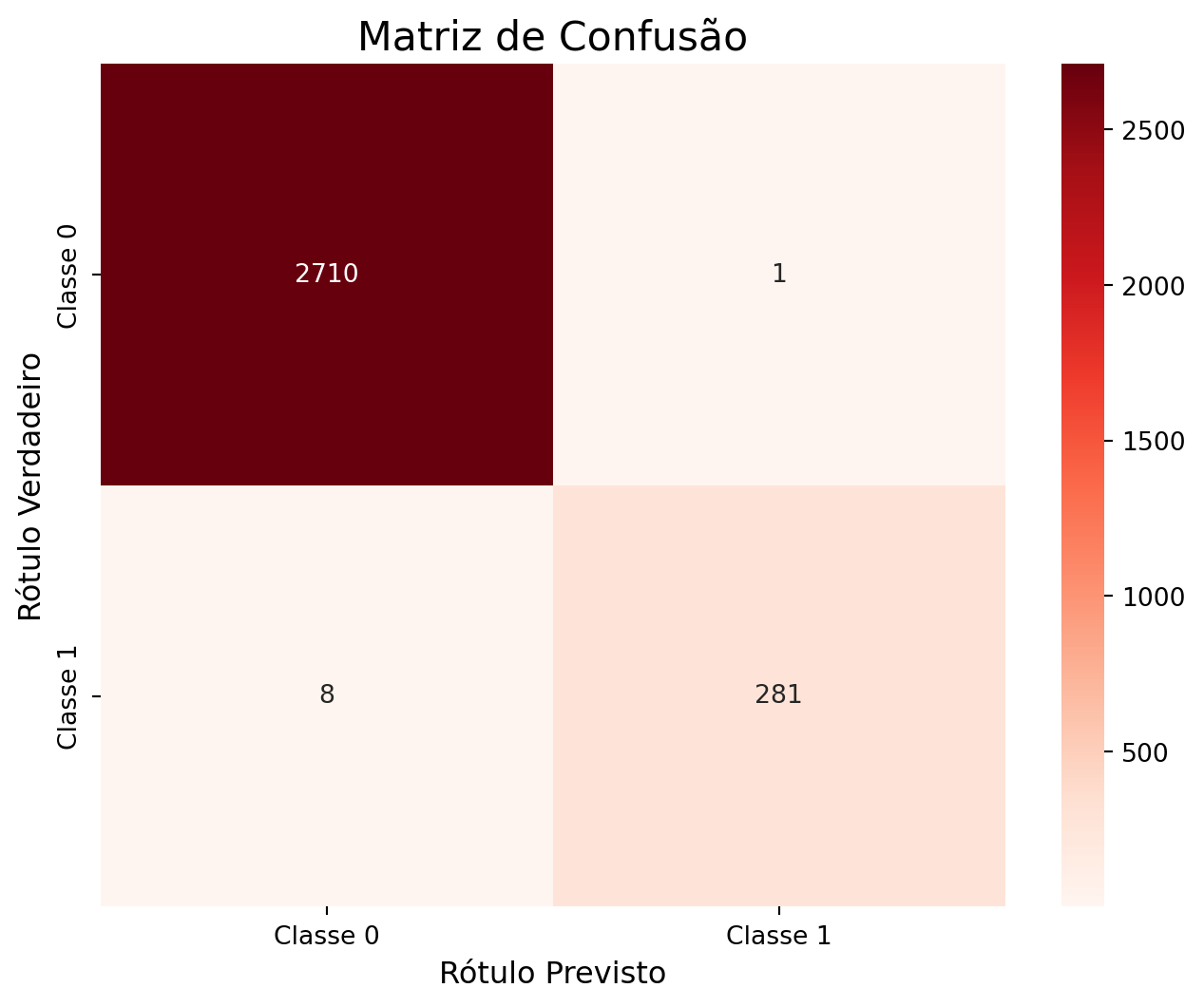

E a curva ROC:

fpr, tpr, thresholds = roc_curve(y_test, y_pred_rf_proba)

plt.figure(figsize=(8, 8))
plt.plot(fpr, tpr, color=colors[0], lw=2, label=f'Curva ROC (AUC = {auc_score_rf:.8f})')
plt.plot([0, 1], [0, 1], color=colors[1], lw=2, linestyle='--', label='Classificador Aleatório')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('Taxa de Falsos Positivos (FPR)', fontsize=12)
plt.ylabel('Taxa de Verdadeiros Positivos (TPR)', fontsize=12)
plt.title('Curva ROC (Receiver Operating Characteristic)', fontsize=16)
plt.legend(loc="lower right")
plt.tight_layout()
plt.show()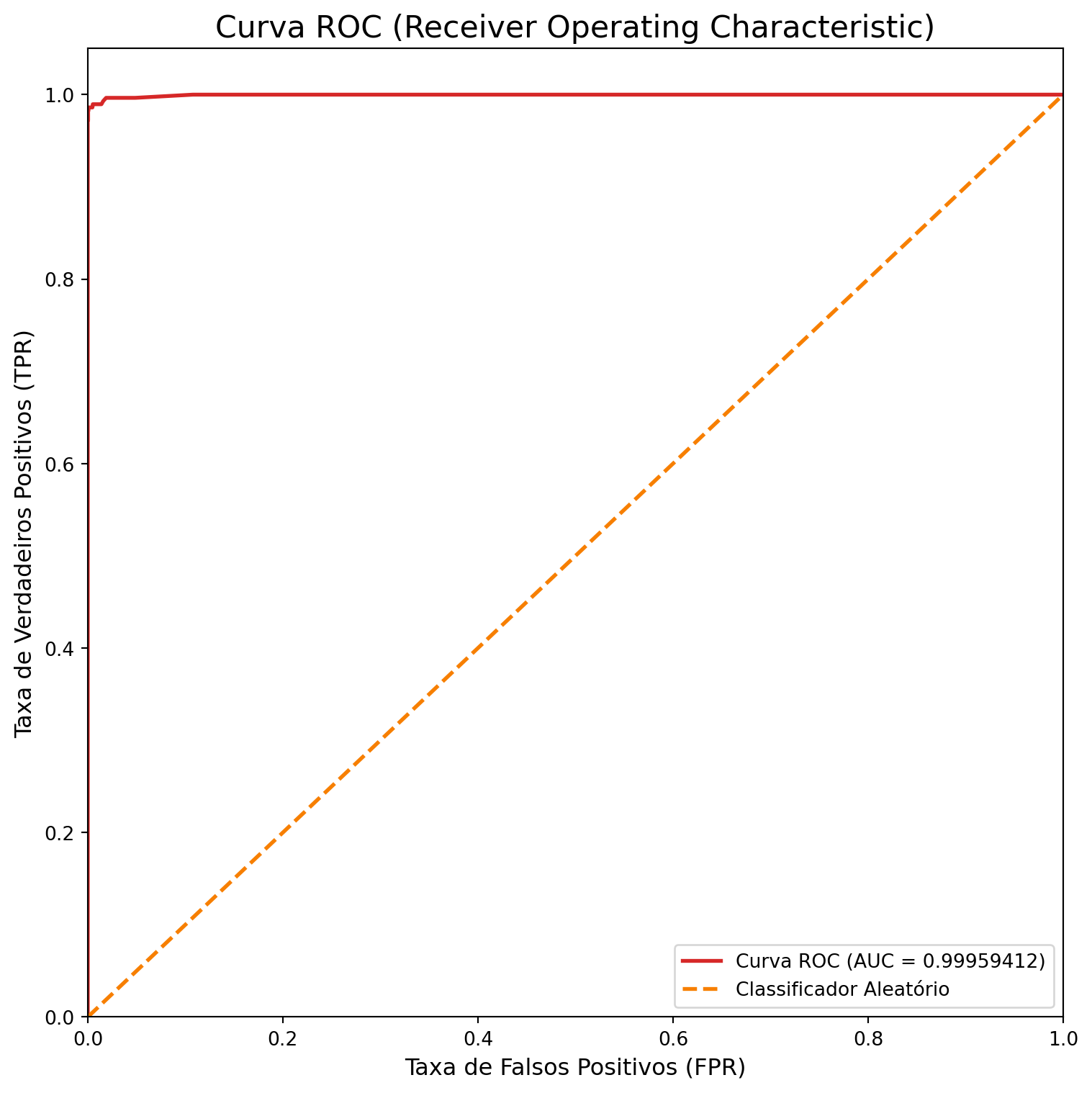

Comparando os modelos

results_data = {
    'Modelo': ['Regressão Logística', 'Árvore de Decisão', 'Random Forest'],
    'Acurácia': [acuracia_logreg, acuracia_tree, acuracia_rf],
    'AUC': [auc_score_logreg, auc_score_tree, auc_score_rf]
}

resultados_df = pd.DataFrame(results_data)

resultados_df

	Modelo	Acurácia	AUC
0	Regressão Logística	0.943000	0.963492
1	Árvore de Decisão	0.995333	0.991128
2	Random Forest	0.997000	0.999594